포트폴리오 최적화는 목표를 이루기 위해 고려하고 있는 모든 포트폴리오 세트 중에서 최상의 포트폴리오(=자산 분배)를 선택하는 프로세스입니다. 목표는 일반적으로 기대 수익과 같은 요소를 최대화하고 재무 위험과 같은 비용을 최소화합니다.
이 포스팅을 통해서 파이썬을 이용한 효율적 투자선(=efficient frontier) 및 주식 포트폴리오를 최적화하는 방법을 설명해 드릴 예정입니다. 현대 포트폴리오 이론에 의하면 효율적 투자선은 위험-수익 스펙트럼에서 '효율적인' 위치에 있는 투자 포트폴리오입니다. 보통은 효율적 투자선은, 수익의 변동성이 동일할때 해당 포트폴리오보다 높은 기대수익을 주는 포트폴리오가 없는 것을 의미합니다.
Sharpe Ratio는 실제로 투자 포트폴리오에서 사용되는 개념이며, 보유한 투자 주식 종목에서 최상의 구성비율을 찾는 데 이용할 수 있는 개념입니다.
Sharpe Ratio는 1966년 William F. Sharpe에 의해 개발되었습니다. Sharpe Ratio는 더 위험한 자산을 보유하기 위해 견뎌야 하는 추가적인 변동성에 대해 얼마나 많은 초과 수익을 얻었는지를 나타냅니다. 위험을 조정 한 후 무위험 자산(채권, 국채 등)과 비교하여 투자 성과를 측정합니다. 투자 수익과 무위험 수익 간의 차이를 투자의 표준 편차로 나눈 값으로 정의됩니다.
상대적으로 적은 위험에 대해 높은 기대 수익률을 내는 투자 포트폴리오는?
일반적으로 1.0보다 큰 Sharpe Ratio는 괜찮은 포트폴리오로 간주됩니다. 2.0보다 높은 비율은 매우 좋음으로 평가됩니다. 3.0 이상의 비율은 우수한 것으로 간주됩니다. 1.0 미만의 비율은 차선책으로 간주됩니다.
그렇다면, Sharpe Ratio가 높은 투자 포트폴리오는 어떻게 구성할 수 있을까요? 이제 실제 파이썬 프로그래밍을 통해서 좋은 투자포트폴리오를 찾아 봅시다!
# 이 프로그램은 효율적 투자선(=Efficient Frontier)과
# 파이썬(Python)을 이용하여사용자 포트폴리오를 최적화합니다.
# 먼저 필요한 라이브러리를 설치합니다.
!pip install -q -U finance-datareader먼저 관련 라이브러리 Import
# Import the python libraries
import FinanceDataReader as fdr
import pandas as pd
import numpy as np
from datetime import datetime
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')가상 포트폴리오 만들기
가상 포트폴리오에 대한 주식 가격 데이터와 티커를 가져옵니다. 이번 포스팅에서는 FAANG로 알려진 가장 인기 있고 실적이 좋은 미국 기술회사 5개를 사용할 것입니다. FAANG를 나타내는 5개 회사는 Facebook, Amazon, Apple, Netflix, Alphabet (이전의 Google)입니다.
assets = ["FB", "AMZN", "AAPL", "NFLX", "GOOG"]
다음으로 가장 기본적인 포트폴리오를 구성해 봄니다. 기본 포트폴리오는 각 주식이 동등한 가중치를 갖도록 설정하면 됩니다. 즉, 이 포트폴리오는 총 5개 종목이 있으니 각 종목별로 20%씩 보유하는 포트폴리오입니다. 즉, 포트폴리오에 총 $100 USD가 있다면 각 주식을 $20 만큼 매수했다고 생각하시면 됩니다.
# Assign weights to the stocks. Weights must = 1 so 0.2 for each
weights = np.array([0.2, 0.2, 0.2, 0.2, 0.2])
weights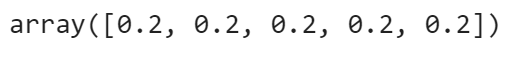
이제 주식 시작일은 2013년 1월 1일이고 종료일은 현재 날짜 (오늘)로 설정합니다.
#Get the stock starting date
stockStartDate = '2013-01-01'
# Get the stocks ending date aka todays date and format it in the form YYYY-MM-DD
today = datetime.today().strftime('%Y-%m-%d')각 주식의 일별 종가 데이터를 저장할 데이터 프레임을 생성합니다.
def fetch_data(assets: list, start_dt: str, end_dt: str) -> pd.DataFrame:
closes = []
for ticker in assets:
fetched_df = fdr.DataReader(ticker, start = start_dt, end = end_dt)
history_df = pd.DataFrame({'Date':fetched_df.index, ticker:fetched_df['Close']})
history_df.set_index('Date', drop=True, inplace=True)
closes.append(history_df)
closes = pd.concat(closes, axis=1)
closes.dropna(inplace=True)
return closes
# Store the adjusted close price of stock into the data frame
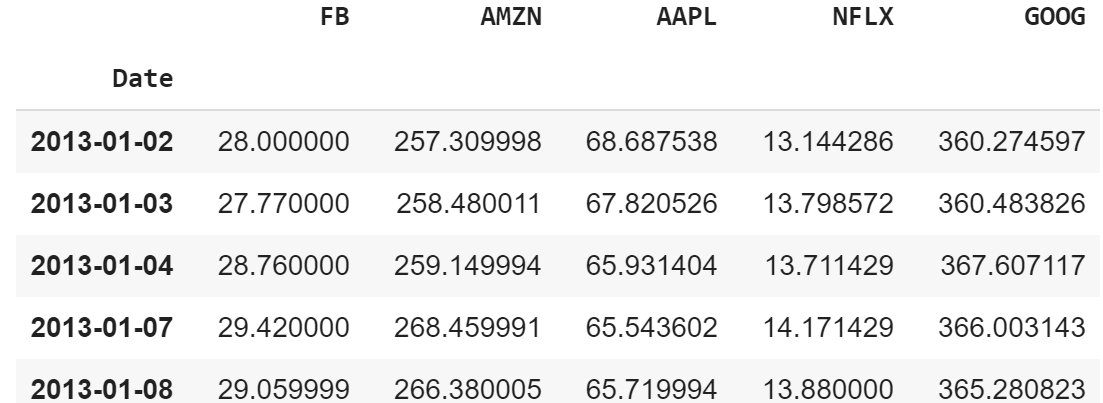
df = fetch_data(assets = assets, start_dt = stockStartDate, end_dt = today)데이터 프레임에 저장된 각 주식의 종가를 살펴보면 다음과 같습니다.
주식 가격이 시간에 따라 어떻게 변했는지 시각화 해보겠습니다.
# Create the title 'Portfolio Adj Close Price History
title = 'Portfolio Close Price History '
#Get the stocks
my_stocks = df
#Create and plot the graph
plt.figure(figsize=(12.2,4.5)) #width = 12.2in, height = 4.5
# Loop through each stock and plot the Adj Close for each day
for c in my_stocks.columns.values:
plt.plot( my_stocks[c], label=c)#plt.plot( X-Axis , Y-Axis, line_width, alpha_for_blending, label)
plt.title(title)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Close Price USD ($)',fontsize=18)
plt.legend(my_stocks.columns.values, loc='upper left')
plt.show()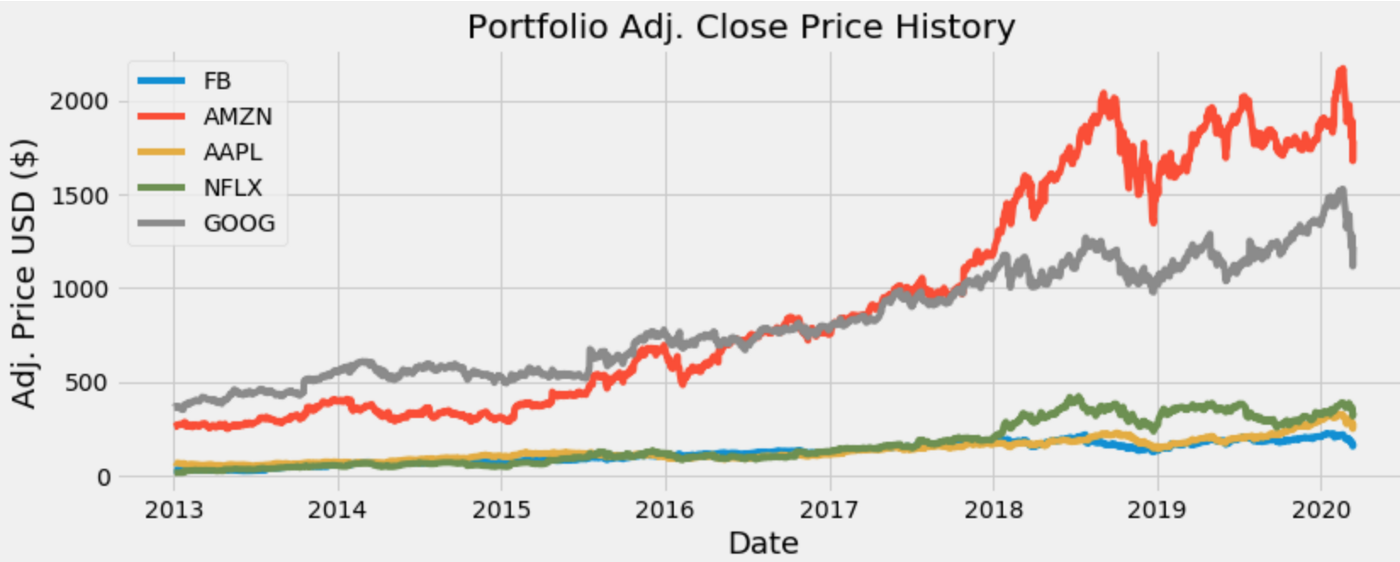
재무 계산
지금까지 가상의 포트폴리오를 만들었습니다. 이제 (new_price +- old_price) / old_price 또는 (new_price / old_price)-1의 계산을 통해 일일 단순 수익률을 표시해 보겠습니다.
#Show the daily simple returns, NOTE: Formula = new_price/old_price - 1
returns = df.pct_change()
returns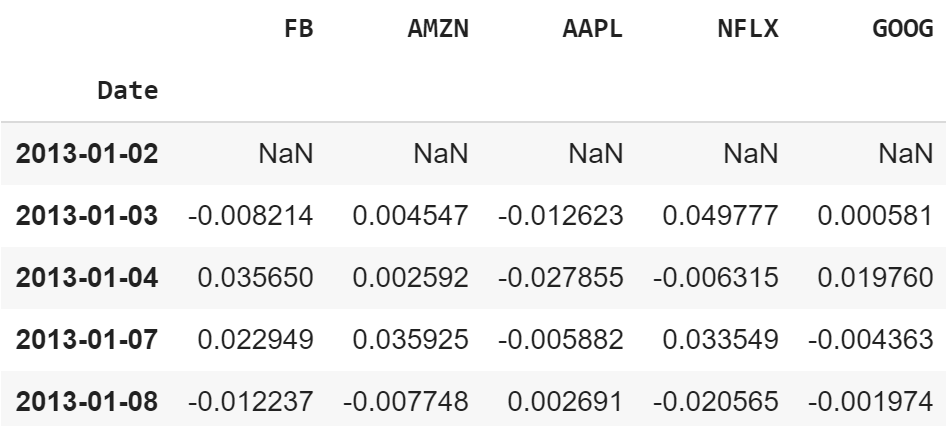
다음으로 연간 공분산 행렬을 계산하고 출력해 보겠습니다. 공분산 행렬은 서로 다른 모집단의 데이터 샘플을 비교할 때 통계에서 일반적으로 사용되는 수학적 개념이며 두 개의 임의 변수가 얼마나 변하거나 함께 이동 하는지를 결정하는 데 사용됩니다. 따라서, 공분산 행렬을 통해서 두 자산 가격간의 방향 관계를 알아 낼 수 있습니다.
행렬의 대각선은 분산이고 다른 항목은 공분산입니다. 분산은 일련의 관측치가 서로 얼마나 다른지 측정합니다. 분산의 제곱근을 취하면 표준 편차라고도하는 변동성을 얻습니다.
연간 공분산 행렬을 표시하려면 공분산 행렬에 현재 연도의 거래 일수를 곱해야합니다. 보통 연간 거래일수는 해마다 다르지만 250일 정도로 계산하면 얼추 비슷합니다. 올해의 거래일수는 252일입니다.
cov_matrix_annual = returns.cov() * 252
cov_matrix_annual
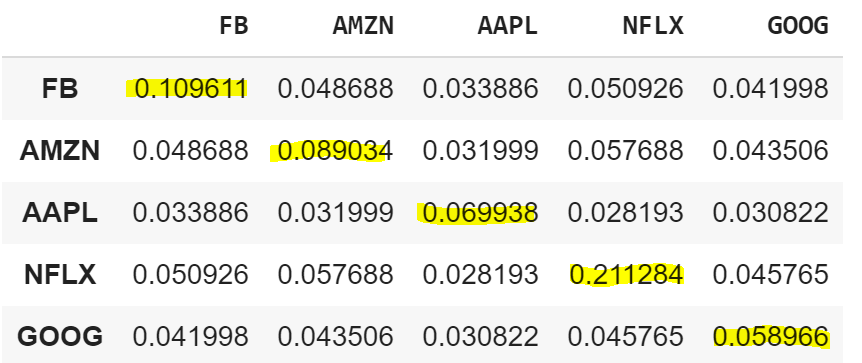
이제 다음 공식을 사용하여 포트폴리오 분산을 계산하고 출력해 보겠습니다.
포트폴리오 분산의 기대값 = WT * (공분산 행렬) * W
port_variance = np.dot(weights.T, np.dot(cov_matrix_annual, weights))
port_variance

이제 다음 공식을 사용하여 포트폴리오 변동성을 계산하고 출력해 보겠습니다.
포트폴리오 변동성의 기대값 = SQRT (WT * (공분산 매트릭스) * W)

변동성(=표준 편차)은 단지 분산의 제곱근이라는 것을 잊지 마십시오.
port_volatility = np.sqrt(port_variance)
port_volatility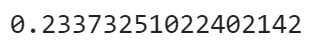
마지막으로 포트폴리오 연간 단순 수익률을 계산하고 출력해보겠습니다.
portfolioSimpleAnnualReturn = np.sum(returns.mean()*weights) * 252
portfolioSimpleAnnualReturn

예상 연간 수익, 변동성 또는 위험 및 분산을 출력해 보겠습니다.
percent_var = str(round(port_variance, 2) * 100) + '%'
percent_vols = str(round(port_volatility, 2) * 100) + '%'
percent_ret = str(round(portfolioSimpleAnnualReturn, 2)*100)+'%'
print("Expected annual return : "+ percent_ret)
print('Annual volatility/standard deviation/risk : '+percent_vols)
print('Annual variance : '+percent_var)
동일한 비중으로 포트폴리오를 구성한 경우, 연간 예상 투자 수익률이 32%이고 이 포트폴리오의 위험이 23%라는 것을 알게 되었습니다. 그렇다면, 이것보다 더 좋은 수익을 얻을 수 있는 방법은 없을까요?
포트폴리오 최적화
이제이 포트폴리오를 최적화 할 때입니다. 즉, 최소한의 위험으로 최대 수익을 최적화하고 싶습니다. 다행히도 Robert Ansrew Martin이 만든 매우 멋진 패키지를 이용하면, 포트폴리오를 쉽게 최적화 할 수 있습니다. 그가 만든 pyportfolioopt라는 패키지를 사용해서 포트폴리오를 최적화 해보겠습니다.
우선 관련 라이브러리를 Import 하겠습니다.
from pypfopt.efficient_frontier import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns
예상 수익률과 일일 자산 수익률의 연간 표본 공분산 행렬을 계산합니다.
mu = expected_returns.mean_historical_return(df)#returns.mean() * 252
S = risk_models.sample_cov(df) #Get the sample covariance matrix최대 Sharpe Ratio를 최적화합니다.
ef = EfficientFrontier(mu, S)
weights = ef.max_sharpe() #Maximize the Sharpe ratio, and get the raw weights
cleaned_weights = ef.clean_weights()
print(cleaned_weights) #Note the weights may have some rounding error, meaning they may not add up exactly to 1 but should be close
ef.portfolio_performance(verbose=True)
이제 우리는 포트폴리오의 Facebook을 15.79%, Amazon을 23.296%, Apple을 25.573%, Netflix를 35.341%, Google을 0% 보유함으로써 이 포트폴리오를 최적화 할 수 있음을 알 수 있습니다.
또한 이 최적화를 통해 예상 연간 수익이 37.6%로 증가했으며 연간 변동성 / 위험이 26.3%임을 알 수 있습니다. 이 최적화 된 포트폴리오는 1.35의 Sharpe 비율을 가지고 있습니다. 하단의 괄호 안의 숫자는 방금 십진수 형식으로 언급 한 세 숫자와 동일합니다.
이제 위의 비율에 따라서 포트폴리오를 구성할때 종목별 몇주씩 매수를 해야 하는지 알고 싶습니다. 즉, 이 포트폴리오에서 각 종목의 할당(discrete allocation)을 정확히 알고 싶습니다.
예를 들어, 저는 이 포트폴리오에 미화 15,000달러를 투자한다고 할때, 최적의 결과를 제공하기 위해 포트폴리오에서 각 주식을 몇주씩 매수해야 할지 알고 싶은 것입니다.
포트폴리오에서 종목의 할당을 계산하이 위해서는 다음과 같이 pulp라는 라이브러리를 설치해야 합니다.
pip install pulp
이제 각 주식의 개별 할당을 계산해 보겠습니다.
from pypfopt.discrete_allocation import DiscreteAllocation, get_latest_prices
latest_prices = get_latest_prices(df)
weights = cleaned_weights
da = DiscreteAllocation(weights, latest_prices, total_portfolio_value=15000)
allocation, leftover = da.lp_portfolio()
print("Discrete allocation:", allocation)
print("Funds remaining: ${:.2f}".format(leftover))

이제 다 됐습니다. 이 최적화된 포트폴리오에 기반해서 미화 15,000달러를 투자한다고 했을때, Facebook 14주, Amazon 2주, Apple 13주, NetFlix 16주를 매수할 수 있으며 이렇게 투자하고 나면 15,000달러 중에서 약 51.67달러가 남게 됩니다.
이게 각자 나름의 포트폴리오를 구성해서 현명하게 투자해 보시기 바랍니다.
원문 읽기:>>click
'데이터과학 > 데이터 분석 실습' 카테고리의 다른 글
| 스토캐스틱 지표를 이용한 알고리즘 투자전략 (feat. 파이썬) (0) | 2020.12.30 |
|---|---|
| 시계열 안정성 테스트 - ADF and KPSS 테스트 (feat. 파이썬) (5) | 2020.12.25 |
| 자금 흐름 지표를 이용한 알고리즘 투자 전략 (feat. 파이썬) (0) | 2020.12.25 |
| OBV 거래량 지표를 이용한 알고리즘 투자 전략 (feat. 파이썬) (1) | 2020.12.25 |
| 이동평균선과 RSI를 이용한 알고리즘 투자전략 (feat. 파이썬) (0) | 2020.12.25 |



